The Sigma Enigma
One hears is a great deal about six-sigma of these days. Today, six-sigma characterizes a form of continual improvement in quality. If you say that this is all Greek to me you are probably correct. The word “sigma” is the Greek letter “σ”, the lowercase “s” in this context. Sigma (σ) is a measure of variation and is also called the “standard deviation”. To understand how the term came about we need to look at how it is computed and how it is used.
The computation of sigma or the standard deviation is best explained by the use of some data. For instance, suppose that we had the results of the same five tests for two students as shown in the table below:
Test |
Paul |
Peter |
1 |
100 |
91 |
2 |
95 |
91 |
3 |
90 |
89 |
4 |
85 |
91 |
5 |
80 |
88 |
Average |
90 |
90 |
Range |
20 |
3 |
Variance |
50 |
1.60 |
Standard Deviation |
7.07 |
1.26 |
The average of Paul’s five tests is clearly 90. The average of Peter’s five tests is also 90. Yet, there is a substantial difference between these test results. The range (the smallest reading subtracted from the largest) of Paul’s five scores is 20 (= 100 – 80). Peter, on the other hand has a range of only 3. This means that Peter is more consistent than Paul. Peter’s results show less variation than do Paul’s results.
From our days in school we are used to averages, grade averages, etc. The average, as everyone knows is obtained by summing the items and dividing the total by the number test scores summed. The average (its technical name is the arithmetic mean) is a convenient way of describing a large set of data or numbers.
From the example it is apparent, however, that the average is not enough to distinguish performance. Peter and Paul had the same average yet the numbers making up the average were quite different. Peter showed far more consistency in his results than did Paul. We use several measure of consistency. Introduced above is a measure called the range.
One way to measure variation is to use the average as a reference point. If we subtract the average from each value and then average the differences, one might think, we can get a measure of variation. Below is a table that shows the results for our example:
Test |
Paul |
Difference from Average |
Peter |
Difference from Average |
1 |
100 |
10 |
91 |
1 |
2 |
95 |
5 |
91 |
1 |
3 |
90 |
0 |
89 |
-1 |
4 |
85 |
-5 |
91 |
1 |
5 |
80 |
-10 |
88 |
-2 |
Average |
90 |
0 |
90 |
0 |
As one can see the average of the difference from the average of a set of numbers is always zero. We could, of course, ignore the signs by taking the average of the absolute values. While this measure finds some use in inventory theory, it does not have the desirable characteristics that we get in another way.
We take advantage of the fact that a number multiplied by itself—a process called squaring the number—always produces a positive result. Thus, Paul’s difference from the average for test #4 was –5. Multiplying –5 times –5 gives +25 (-5 * -5 = 25). We call the average of the squared differences the Variance of the data. The table below shows the computation for Paul’s data:
Test |
Paul |
Difference from Average |
Squared Difference |
1 |
100 |
10 |
100 |
2 |
95 |
5 |
25 |
3 |
90 |
0 |
0 |
4 |
85 |
-5 |
25 |
5 |
80 |
-10 |
100 |
Average |
90 |
0 |
50 |
Paul’s variance is 50. To obtain this value, the differences were squared. In order to bring the measure of variation to the original number scale, we reverse the process of squaring, called taking a square root. Most calculators today have a square root key with the symbol 
. Entering a number, then pressing the square root key results in a number which when multiplied by itself gives the original square. The square root of 50 is 7.0711… The three dots, or ellipses, indicate that there are more figures following the number. In short, 7.0711 times 7.0711 equals 50.0.
|
The square root of the variance is known as the standard deviation. This is the sigma that we talk about. When dealing with a population it is the square root of the average of the differences squared. When dealing with a sample from a population we make an adjustment to the average by dividing the sum of the squares by the number of items summed less one.
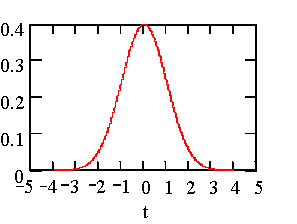
So what? Where is sigma? We are getting there. When dealing with a population, we call the standard deviation, sigma. This sigma has special properties when the population has a distribution that is popularly called the bell shaped curve and more officially known as the Gaussian or Normal distribution. The figure on the left shows the Normal distribution in terms of standard deviations or sigma’s. The mean at 0 sigma is in the center. Notice that when we are dealing with the Normal distribution that the curve from –3-sigma to +3-sigma, covers nearly all of the area under the curve.
The Normal distribution has been studied and the area under the curve of the distribution from minus infinity to some sigma value has been tabulated. In this way, it is possible to determine the area under the curve for any mean plus or minus t standard deviations. Some basic measures are generally known. The following are common:
t-sigma |
Approximate area |
|
68% |
|
90% |
|
95% |
|
99.0% |
|
99.73% |
|
99.9936% |
|
99.99932% |
Of course, if the underlying distribution is not the Normal distribution, these values do not hold. Some other area under the curve would apply
When Walter Shewhart invented the process control chart in the mid 1920’s, he was faced with making two mutually exclusive mistakes in using the chart. Mistake one was to say that the process needed fixing, when it was operating normally. Mistake two was to say that the process was operating normally when it really needed fixing. By always fixing (tinkering, tampering?) with the process he could avoid mistake number two. The penalty was that he made mistake number one the maximum number of times. How to balance these two mistakes?
Shewhart found that there was no theoretical solution available to him. He did not know the underlying distribution of the process. Nor was this very important to him. What he did was to experiment using several distributions, the
He then applied several models to see which gave him the most economic balance between the two mistakes. He found that the model of the average plus or minus three standard deviations gave him the best results, regardless of the underlying distribution. We have been using this model ever since. It works!
So what has the Shewhart model of the average plus or minus three-sigma to do with six-sigma? In a mistaken view of the Shewhart Chart people at Motorola thought that the chart showed the probability of permitting defects to escape from a process. They also thought that a process average could shift ±1.5-sigma while the process is in control. Neither of these situations is possible in a stable system. Since the underlying distribution is not known, no probability statements are possible. Without such statements, no one can say what is the exact probability of a given point plotted on a control chart. The second issue is based on a misunderstanding of what a control chart could or could not do. The whole point of a Shewhart chart is to indicate a process average shift. When such shifts occur, the chart signals that a special cause of variation is present.
Not realizing this, the people at Motorola thought that their processes should be tighter, so tight that the even a ±1.5 sigma shift in the process average yields no more than 3.4 parts per million defective. They called this process six-sigma. The writer learned that it was Motorola’s CEO, General Galvin who either originated or approved the term six-sigma.
In the past few years, Mr. Jack Welch, CEO of General Electric (GE) has popularized the concept of six-sigma. Mr. Welch added a factor to the desire for continual improvement, cost benefit. In the GE use of the concept it is necessary to show that there will be a cost benefit to the company.
The use of anything that will logically improve quality is useful. In the case of six-sigma, Motorola engaged in a process that was good for the wrong reason. The number of sigmas in a process is not as significant to an organization as is the consistency of the process. A control chart gives the measure of predictability of a process, which in turn can give us the economic value of the process. It is no accident that the tools used to accomplish that goal are the tools that were used previously. The one benefit of using the term “six-sigma” seems to be that today more companies are using not merely Ishikawa’s seven elementary tools but are also applying the intermediary and advanced tools he outlines in his book, What is Total Quality Control? The
Is there a possible downside to this? Yes. In a 1995 paper, the writer discusses the possibility of spinning wheels at considerable cost. This paper can be found on this web site as www.latzko-associates.com/Publications/SIX_Sig.pdf.
In summary then, six-sigma is a term that today describes continual improvement. It is derived from the concept of the measure of variation and was originally devised to overcome a falsely perceived shortcoming in the Shewhart Chart.